Deuxième partie
par Daniel MARTY
La gamme de Pythagore
Dans la Grèce antique, Pythagore a étudié le rapport entre les longueurs de cordes et les fréquences et a établi une gamme sur cette base. La quinte a une origine naturelle (cordes vibrantes, colonnes d’air…) et peut être déterminée à l’oreille par les musiciens. Le rapport concerné est de 3/2.
Dans la gamme de Pythagore les notes s’obtiennent par quintes successives à partir d’une note de référence. L’octave a la propriété de contenir 8 notes avec N=2 à l‘octave. Il faut donc trouver 6 notes dont les fréquences soient comprises entre N1 et 2N1 à partir de quintes successives N2/N1= 3/2 etc….
On aura donc pour la suite d’octaves : Do1 X 2 → Do2 , Do2 X 2 → Do3 etc.
Par ailleurs, on aura pour la suite des quintes :
Fréquence Do1 X 3/2 → Sol1
Fréquence Sol1 X 3/2 → Ré2
Fréquence Ré2 X 3/2 → La2 etc .
Si on continue de multiplier les fréquences par 3/2 à partir de la note Si on obtiendra successivement Fa#, Do#, Sol#, Ré#…. soit :
Do Sol Ré La Mi Si Fa# Do# Sol# Ré# La# Fa Do
et en divisant par 3/2 à partir de Fa :
Do Fa Sib Mib Lab Réb Solb Si Mi La Ré Sol Do
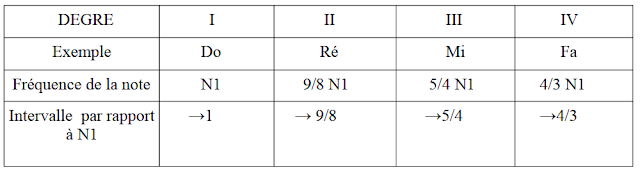
On aura alors les intervalles suivants, sachant que l’on obtient ces intervalles en faisant le rapport des fréquences successives:
Le Do, que l’on pensait avoir à la fin du cycle des quintes montantes, ne coïncide pas tout à fait avec le Do du départ. Par ailleurs, une note bémolisée ne coïncide pas tout à fait avec la
note diésée inférieure. Ainsi Fa# est légèrement plus bas que Solb.
Cela conduit au fait que les instruments à clavier et les guitares, par exemple, qui ont des frettes, ne peuvent pas être accordés de manière parfaitement juste. Il faut donc trouver un compromis. Ce compromis ce sera le tempérament égal qui consiste à diviser la gamme en 12 demi-tons égaux. Par contre, la gamme harmonique peut être restituée par les instruments de la famille des violons. Le violon étant accordé par quinte il s’agit d’un instrument »Pythagorien ».
Cette gamme est remarquable par la constance de ses intervalles mais malheureusement n’est pas cyclique, le Si# ne coïncide pas avec le Do à l’octave. La transposition, bien que difficile, est néanmoins possible. Le cycle ne se referme donc pas et certains sons ne sont pas parfaitement purs. Cette gamme est parfaite pour les lignes mélodiques et est la plus expressive. Les musiciens qui peuvent faire leurs notes, tels que les violonistes, jouent une gamme très proche de la gamme de Pythagore. Elle n’est pas envisageable pour les instruments à sons fixes tels que le piano ou… l’harmonica.
La gamme de Zarlino
Au XVIème siècle, Giosetto Zarlino propose une gamme basée sur les harmoniques naturelles. Il envisage alors des harmoniques particuliers émis simultanément (accords) qui sont des multiples de la note fondamentale. Zarlino a construit sa gamme à partir d’accords parfaits majeurs. Ces accords sont naturels et peuvent être déterminés scientifiquement, ou à l’oreille, par les musiciens. Cette gamme est construite par une succession d‘accords parfaits majeurs (Do Mi Sol – Sol Si Ré – Fa La Do) constitués chacun d’une tierce (majeure) et d’une quinte (juste). Si N est la fréquence du premier son de l’accord, 5/4 de N sera la fréquence du deuxième son de l’accord et 3/2 de N la fréquence du troisième son de l’accord.
DO (1) MI (5/4) SOL (3/2)
Soit N la fréquence d’un son. L’octave doit contenir 8 notes : N1, N2, N3….., N8 avec N8 = 2N1. Il faut donc trouver 6 notes qui seront obtenues à l’aide de 3 accords parfaits. L’accord parfait construit sur N1 donne 2 notes, l’une de ces notes étant la première note de l‘accord parfait suivant qui permet d’obtenir 2 nouvelles notes. Un troisième accords parfait construit
sur l’une des notes fournira les deux dernières notes. On trouvera, consignés dans le tableau suivant, les résultats ainsi obtenus.
La structure de l’octave de Zarlino est celle qui se rapproche le plus de la structure de l’octave de Pythagore. Dans la gamme de Pythagore on avait deux valeurs d’intervalles, 9/8 pour le ton et 16/15 pour le demi-ton. On a ici deux valeurs différentes pour le ton : 9/8 pour Do-Ré, Fa-Sol, La-Si et 10/9 pour les intervalles de ton Ré-Mi et Sol-La.
Cette gamme, plus proche de l’harmonie naturelle que celle de Pythagore est particulièrement pure au niveau de la mélodie et des accords mais elle entraine des valeurs d’intervalles différentes selon les tonalités et est donc difficilement transposable. Par exemple, l‘intervalle de quinte Ré-La en tonalité de Ré comporte un comma de moins que l‘intervalle de quinte Do-Sol en tonalité de Do.
Pour assurer une plus grande justesse, lors des transpositions, on a été conduit à définir des altérations différentes selon qu’elles montent ou qu’elles descendent. Ainsi, au XVIème siècle ont été réalisés des clavecins à deux claviers sur lesquels les notes baissées (ex : Réb) étaient différentes des notes montées (ex: Do#) de la valeur d’un comma. Ce problème sera supprimé au XVIIème siècle avec l’apparition de la gamme tempérée.
* Comma: 1/9ème de ton.
Avec l’aimable
autorisation de H2F Harmonica de France